Capítulo 8 \(ARMA(p,q)\): Proceso Autoregresivo de Medias Móviles
Es muy probable que una serie de tiempo \(X_t\), tenga características de un proceso \(AR\) y de un proceso \(MA\) al mismo tiempo, por lo que será un proceso \(ARMA\). Así, \(X_t\) sigue un proceso \(ARMA(p,q)\), y en este proceso habrá \(p\) términos autoregresivos y \(q\) términos de media móvil. Este se verá de la siguiente forma:
\[ X_t=c+ \phi_1X_{t-1}+...+\phi_pX_{t-p}-\theta_1\epsilon_{t-1}-\theta_2\epsilon_{t-2}-...-\theta_q\epsilon_{t-q}+\epsilon_t \]
donde \(\epsilon_t\) es un proceso de ruido blanco, y \(\phi_1,...,\phi_p,\theta_1,...,\theta_q\) son los parámetros del modelo.
Para un proceso \(ARMA(p,q)\) una condición de estacionariedad es la misma que para un proceso \(AR(p)\), y una condición de invertivilidad es la misma que para el proceso \(MA(q)\).
El modelo \(ARMA(p,q)\) se puede escribir en términos de los operadores de retardo de la siguiente manera.
Sea \(c = 0\).
\[ \begin{array}{c} (1-\phi_1B-\phi_2B^2-...-\phi_pB^p)X_t=(1-\theta_1B-\theta_2B^2-...-\theta_qB^q)\epsilon_t\\ \implies \phi_p(B)X_t=\theta_q(B)\epsilon_t \end{array} \]
Donde:
- \(\phi_p(B)\) es el polinomio autoregresivo
- \(\theta_q(B)\) es el polinomio de medias móviles.
Hay que observar lo siguiente:
\[ \begin{array}{lr} X_t = \frac{\theta_q(B)}{\phi_p(B)}\epsilon_t & \longleftarrow MA(\infty)\\ \epsilon_t = \frac{\phi_1(B)}{\theta_q(B)}X_t & \longleftarrow AR(\infty) \end{array} \]
- Los modelos \(ARMA(p,q)\) siempre compartirán las características de los modelos \(AR(p)\) y \(MA(q)\), ya que contiene ambas estructuras a la vez.
- El modelo \(ARMA(p,q)\) tiene media cero y varianza constante y finita además de que la función de autocorrelación es infinita y decrece rápidamente hacia cero.
- Un proceso \(ARMA(p,q)\) es estacionario si y sólo si la parte \(MA\) es estacionaria (la suma de los coeficientes en valor absoluto es finita); y la parte \(AR\) también es estacionaria (las raíces del polinomio \(\phi_p(B)\) están fuera del círculo unitario).
- Un proceso \(ARMA(p,q)\) es invertible si y sólo si ambas partes \(AR\) y \(MA\) son invertibles (las raíces de los polinomios \(\phi_p(B)\) y \(\theta_q(B)\) están fuera del círculo unitario).
Ejemplo
Sea \(Y_t: ARMA(2,1)\) con \(\epsilon_t\sim N(0,1)\) tal que \(Y_t = 1.5Y_{t-1}-0.9Y_{t-2}-0.4\epsilon_{t-1}+\epsilon_t\).
Sabemos que la parte del \(MA\) es invertible por que \(|\theta| = |-0.4|<1\) y por lo tanto también es estacionario.
Mientras que en la parte del \(AR\) tenemos:
\[ \begin{split} &\phi_2(B) = (1-1.5B+0.9B^2)\\ \implies & B_1, B_2 = \frac{1.5\pm\sqrt{1.5^2-4(0.9)}}{2(0.9)} = 0.83\pm0.645\\ \implies & |B_1| = 1.475 > 1\\ \implies & |B_2| = 0.185 < 1 \end{split} \] Por lo tanto no es estacionario y tampoco invertible.
8.1 \(ARMA(1,1)\)
En un modelo \(ARMA(1,1)\) la serie de tiempo \(X_t\) se determina en función de su pasado hasta el primer retardo, la innovación actual y el pasado de la innovación hasta el primer retardo.
\[ X_t=c+ \phi_1X_{t-1}+\epsilon_t-\theta_1\epsilon_{t-1} \]
donde \(\epsilon_t\) es un proceso de ruido blanco, y \(\phi_1\) y \(\theta_1\) son los parámetros del modelo. Ahora se verán las características de un proceso \(ARMA(1,1)\) estacionario.
8.1.1 Media
\[ \begin{array}{l} \mathbb{E}(X_t)=\mathbb{E}(c+ \phi_1X_{t-1}+\epsilon_t-\theta_1\epsilon_{t-1})=c+ \phi_1\mathbb{E}(X_{t-1})\\ \end{array} \]
Por lo que Suponiendo estacionariedad \(\mathbb{E}(X_t) = \frac{c}{1-\phi_1}\).
8.1.2 Covarianzas
Recordando que \(\mathbb{E}(X_t) = c+ \phi_1\mathbb{E}(X_{t-1}) \implies X_t-\mathbb{E}(X_t) = \phi_1(X_{t-1}-\mathbb{E}(X_{t-1}))+\epsilon_t+\theta_1\epsilon_{t-1}\)
\[ \begin{split} \gamma_0 &=\mathbb{E}\left[(X_t-\mathbb{E}(X_t))^2\right]\\ &=\mathbb{E}\left[(\phi_1(X_{t-1}-\mathbb{E}(X_{t-1}))+\epsilon_t+\theta_1\epsilon_{t-1})^2\right]\\ &=\mathbb{E}\left[(\phi_1(X_{t-1}-\mathbb{E}(X_{t-1})))^2+2(\phi_1(X_{t-1}-\mathbb{E}(X_{t-1})))(\epsilon_t+\theta_1\epsilon_{t-1})+(\epsilon_t+\theta_1\epsilon_{t-1})^2\right]\\ &=\phi_1^2\mathbb{E}\left[(X_{t-1}-\mathbb{E}(X_{t-1}))^2\right]+2\phi_1\theta_1\mathbb{E}\left[X_{t-1}\epsilon_{t-1}\right]+\mathbb{E}\left[(\epsilon_t+\theta_1\epsilon_{t-1})^2\right]\\ &=\phi_1^2Var(X_{t-1})+2\phi_1\theta_1\mathbb{E}\left[X_{t-1}\epsilon_{t-1}\right]+\mathbb{E}[\epsilon_t^2]+2\theta_1\mathbb{E}[\epsilon_t\epsilon_{t-1}]+\mathbb{E}[\theta_1^2\epsilon_{t-1}^2]\\ &=\phi_1^2Var(X_{t-1})+2\phi_1\theta_1\sigma^2+\sigma^2+\theta_1^2\sigma^2\\ \Longleftrightarrow & (1-\phi_1^2)Var(X_t) = \sigma^2(1+\theta_1^2+2\phi_1\theta_1)\\ \implies & Var(X_t) = \gamma_0 = \frac{\sigma^2(1+\theta_1^2+2\phi_1\theta_1)}{1-\phi_1^2} \end{split} \]
\[ \begin{split} \gamma_1 & =\mathbb{E}[(X_t-\mathbb{E}(X_t))(X_{t-1}-\mathbb{E}(X_{t-1}))]\\ & = \mathbb{E}\left[(\phi_1(X_{t-1}-\mathbb{E}(X_{t-1}))+\epsilon_t+\theta_1\epsilon_{t-1})(X_{t-1}-\mathbb{E}(X_{t-1}))\right]\\ & = \mathbb{E}\left[\phi_1(X_{t-1}-\mathbb{E}(X_{t-1}))^2\right] + \mathbb{E}\left[\epsilon_tX_{t-1}\right]-\mathbb{E}\left[\epsilon_t\mathbb{E}(X_{t-1})\right]+\theta_1\mathbb{E}\left[\epsilon_{t-1}X_{t-1}\right]-\theta_1\mathbb{E}[\epsilon_{t-1}\mathbb{E}(X_{t-1})]\\ &= \phi_1\gamma_0+\theta_1\mathbb{E}[\epsilon_{t-1}X_{t-1}]\\ &= \phi_1\gamma_0 + \theta_1\mathbb{E}[\epsilon_{t-1}(c+\phi_1X_{t-2}+\epsilon_{t-1}+\theta_1\epsilon_{t-2})]\\ &= \phi_1\gamma_0 +\theta_1\mathbb{E}\left[c\epsilon_{t-1}+\epsilon_{t-1}\phi_1X_{t-2}+\epsilon_{t-1}^2+\theta_1\epsilon_{t-1}\epsilon_{t-2}\right]\\ &= \phi_1\gamma_0+\theta_1\sigma^2 \end{split} \]
\[ \begin{split} \gamma_2 & =\mathbb{E}[(X_t-\mathbb{E}(X_t))(X_{t-2}-\mathbb{E}(X_{t-2}))]\\ & = \mathbb{E}\left[(\phi_1(X_{t-1}-\mathbb{E}(X_{t-1}))+\epsilon_t+\theta_1\epsilon_{t-1})(X_{t-2}-\mathbb{E}(X_{t-2}))\right]\\ & = \mathbb{E}\left[(\phi_1(X_{t-1}-\mathbb{E}(X_{t-1}))(X_{t-2}-\mathbb{E}(X_{t-2}))+\epsilon_t(X_{t-2}-\mathbb{E}(X_{t-2}))+\theta_1\epsilon_{t-1}(X_{t-2}-\mathbb{E}(X_{t-2}))\right]\\ &= \mathbb{E}\left[(\phi_1(X_{t-1}-\mathbb{E}(X_{t-1}))(X_{t-2}-\mathbb{E}(X_{t-2}))\right]\\ & \ \ \ \ \ + \mathbb{E}[\epsilon_tX_{t-2}]-\mathbb{E}[\epsilon_t\mathbb{E}(X_{t-2})]+\theta_1\mathbb{E}[\epsilon_{t-1}X_{t-2}]-\theta_1\mathbb{E}[\epsilon_{t-1}\mathbb{E}(X_{t-2})]\\ &= \phi_1\gamma_1 \end{split} \]
Entonces la función de autocovarianza de un proceso \(ARMA(1,1)\) es:
\[ \gamma_{k} = \begin{cases} \frac{\sigma^2(1+\theta_1^2+2\phi_1\theta_1)}{1-\phi_1^2} & k=0\\ \phi_1\gamma_0+\theta_1\sigma^2 & k=1\\ \phi_1\gamma_{k-1} & k>1 \end{cases} \] Y la función de autocorrelación de un proceso \(ARMA(1,1)\) es:
\[ \rho_{k} = \begin{cases} 1 & k=0\\ \frac{\phi_1\gamma_0+\theta_1\sigma_2}{\gamma_0}=\phi_1+\frac{\theta_1\sigma^2}{\gamma_0} & k=1\\ \frac{\phi_1\gamma_{k-1}}{\gamma_0} = \phi_1\rho_{k-1} & k>1 \end{cases} \] A continuación se muestran los resultados para un modelo \(ARMA(1,1)\) de la siguiente forma \(X_t=0.65X_{t-1}+.30\epsilon_{t-1}\)
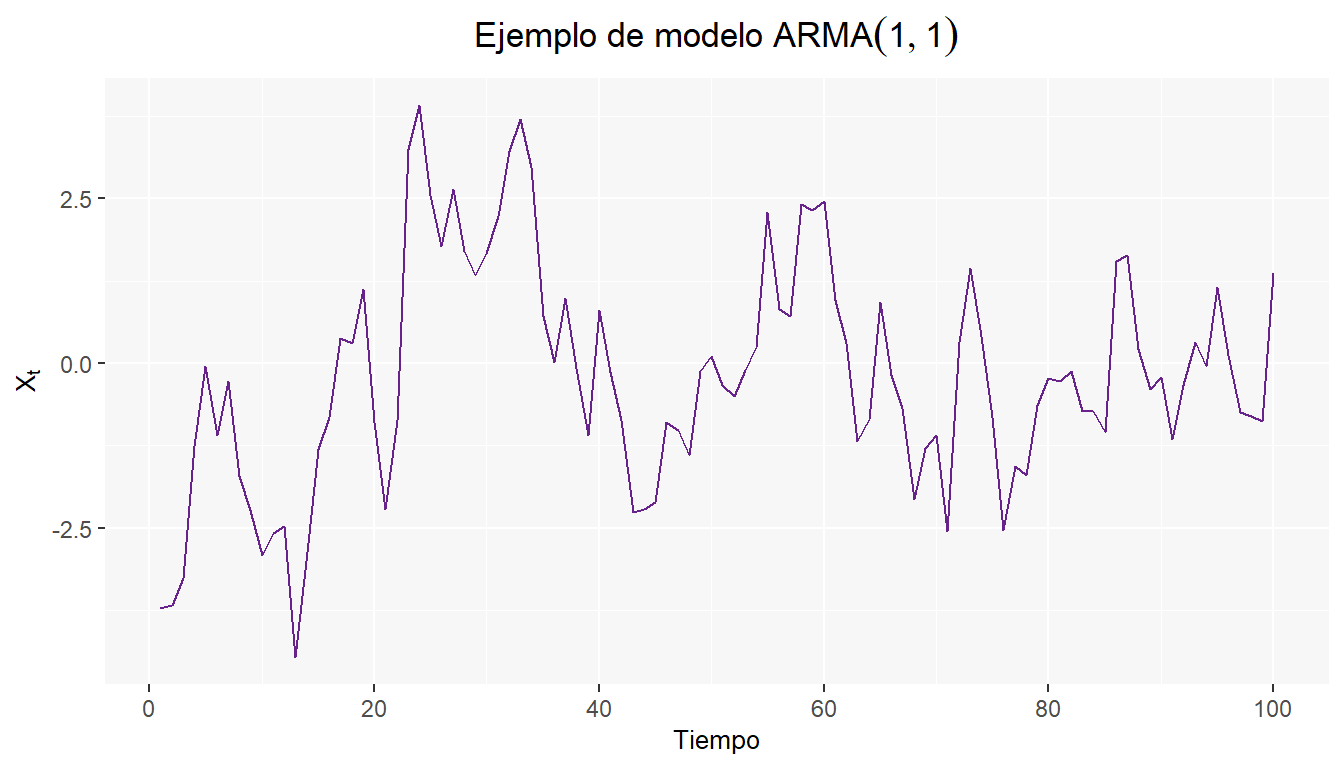
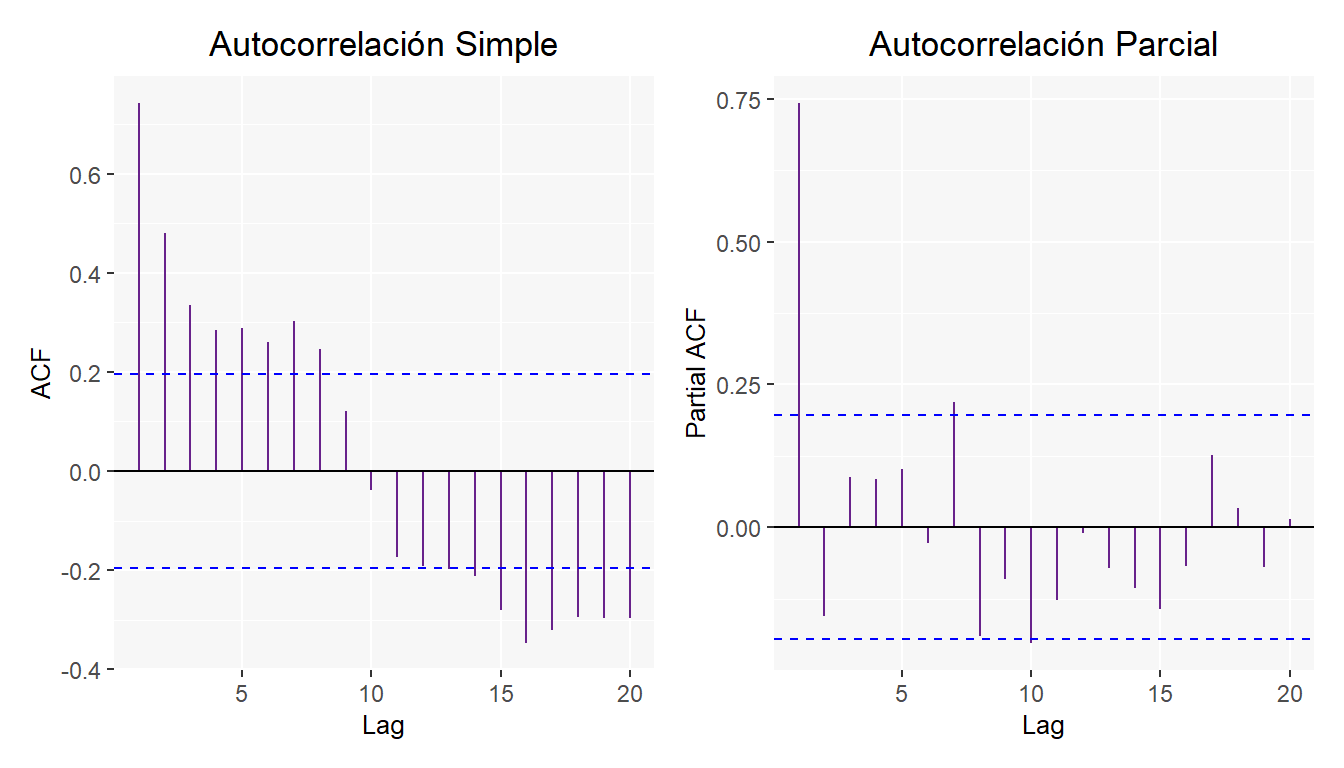
Además de las gráficas de Autocorrelación simple y parcial.
La sección especializada a este tema en el blog es el apartado ARMA.
8.2 Ejericios
- Los modelos \(ARMA(p,q)\) tienen componente autoregresivo y componente de medias móviles
- Cierto
- Falso
- Sólo si p y q son mayores a cero
- Sólo si p y q son distintos de cero
- En un modelo definido por \(X_t=0.65X_{t-1}+\epsilon_t+0.30\epsilon_{t-1}\) con \(\epsilon_t\sim N(0,1)\), calcular \(\rho_2\)
- Suponga que el correlograma de una serie de tiempo con 100 observaciones tiene: \(\hat\rho_1\) = 0.31, \(\hat\rho_2\) = 0.07, \(\hat\rho_3\) = -0.05, \(\hat\rho_4\)= 0.06, \(\hat\rho_5\) = -0.03, \(\hat\rho_6\) = 0.27, \(\hat\rho_7\) = 0.08, \(\hat\rho_8\)= 0.05, \(\hat\rho_9\) = 0.02, \(\hat\rho_10\)= -0.01.¿Qué modelo ARMA es apropiado?